Alternating direction method of multipliers (ADMM)

交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）是一种解决可分解凸优化问题的简单方法，尤其在解决大规模问题上卓有成效，利用ADMM算法可以将原问题的目标函数等价的分解成若干个可求解的子问题，然后并行求解每一个子问题，最后协调子问题的解得到原问题的全局解。ADMM 最早分别由 Glowinski & Marrocco 及 Gabay & Mercier 于 1975 年和 1976 年提出，并被 Boyd 等人于 2011 年重新综述并证明其适用于大规模分布式优化问题。由于 ADMM 的提出早于大规模分布式计算系统和大规模优化问题的出现，所以在 2011 年以前，这种方法并不广为人知。

gnn 聚合和组合

https://towardsdatascience.com/what-can-you-do-with-gnns-5dbec638b525

img

Any GNN can be represented as a layer containing two mathematical operators, aggregation function and combination function. This is best understood using the MPNN (message passing neural network) framework.

aggregation: each message is normalized by sequare root of product of degrees of v and u 也就是把上一层的邻接点的特征向量聚合(归一化), 聚合方法可以使平均, 最大, 最小等 例如 节点 6 的节点1 聚合 a61=X1/(sqrt(7*2)), 其中 X1 是节点 1 的特征, 7 是节点 6 的度, 2 是节点 1 的度

combinetion: 把当前节点的上一层的特征值和本层当前节点的聚合特征 组合

this can be easily achieved by D(-1/2)XAD(-1/2) Usually, Adjacency matrix is added with I (identity matrix) to incorporate node’s own features.

每增加一层, 聚合的信息就多一跳(一层就是节点和他的邻居, 两层就再加上邻居的邻居)

L1 L2 正则化

img

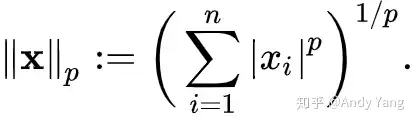
p=1 p=2 代表 L1, L2

因为机器学习中众所周知的过拟合问题，所以用正则化防止过拟合，成了机器学习中一个非常重要的技巧。

但数学上来讲，其实就是在损失函数中加个正则项（Regularization Term），来防止参数拟合得过好。

支持向量机

SVM是什么? 先来看看维基百科上对SVM的定义:

支持向量机（英语：support vector machine，常简称为SVM，又名支持向量网络）是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。给定一组训练实例，每个训练实例被标记为属于两个类别中的一个或另一个，SVM训练算法创建一个将新的实例分配给两个类别之一的模型，使其成为非概率二元线性分类器。SVM模型是将实例表示为空间中的点，这样映射就使得单独类别的实例被尽可能宽的明显的间隔分开。然后，将新的实例映射到同一空间，并基于它们落在间隔的哪一侧来预测所属类别。

如果从未接触SVM的话，维基的这一大段解释肯定会让你一头雾水。简单点讲，SVM就是一种二类分类模型，他的基本模型是的定义在特征空间上的间隔最大的线性分类器，SVM的学习策略就是间隔最大化。

决策树

决策树是一种十分常用的分类方法，需要监管学习（有教师的Supervised Learning），监管学习就是给出一堆样本，每个样本都有一组属性和一个分类结果，也就是分类结果已知，那么通过学习这些样本得到一个决策树，这个决策树能够对新的数据给出正确的分类。

卷积

https://www.zhihu.com/question/22298352

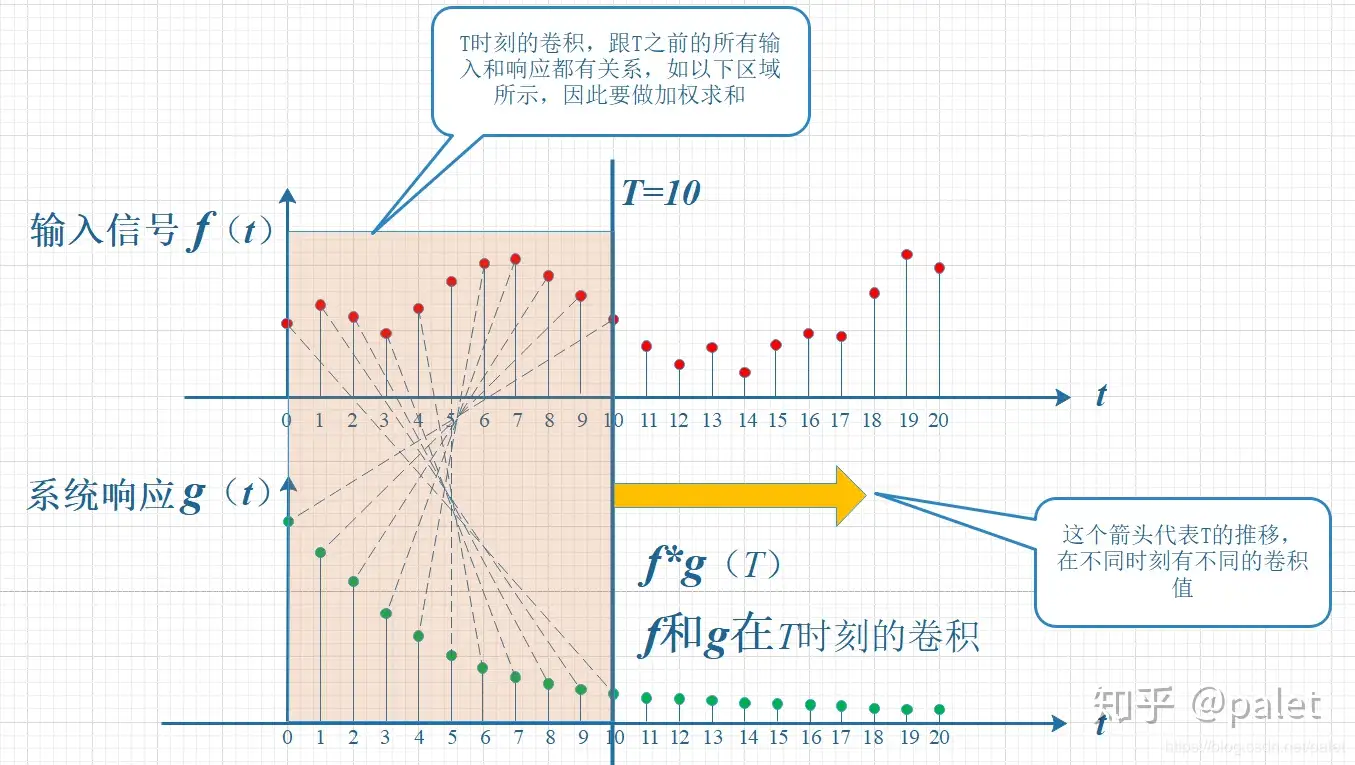
对卷积这个名词的理解：所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加。

img

神经网络

简单神经网络架构

基本神经网络的相互连接的人工神经元分为三层：

  • 输入层

    来自外部世界的信息通过输入层进入人工神经网络。输入节点对数据进行处理、分析或分类，然后将其继续传递到下一层。

  • 隐藏层

    隐藏层从输入层或其他隐藏层获取其输入。人工神经网络可以具有大量的隐藏层。每个隐藏层都会对来自上一层的输出进行分析和进一步处理，然后将其继续传递到下一层。

  • 输出层

    输出层提供人工神经网络对所有数据进行处理的最终结果。它可以包含单个或多个节点。例如，如果我们要解决一个二元（是/否）分类问题，则输出层包含一个输出节点，它将提供 1 或 0 的结果。但是，如果我们要解决一个多类分类问题，则输出层可能会由一个以上输出节点组成。

深度神经网络架构

深度神经网络又名深度学习网络，拥有多个隐藏层，包含数百万个链接在一起的人工神经元。名为权重的数字代表节点之间的连接。如果节点之间相互激励，则该权重为正值，如果节点之间相互压制，则该权重为负值。节点的权重值越高，对其他节点的影响力就越大。 从理论上讲，深度神经网络可将任何输入类型映射到任何输出类型。但与其他机器学习方法相比，它们也需要更多大量的训练。它们需要数百万个训练数据示例，而不像较简单的网络那样，可能只需数百或数千个训练数据示例。

分类

前馈神经网络

前馈神经网络以从输入节点到输出节点的单向方式处理数据。一层中的每个节点均与下一层中的每个节点连接。前馈网络使用反馈流程随着时间推移改进预测。

反向传播算法

人工神经网络使用校正反馈循环不断学习，以改进其预测分析。简而言之，您可以认为数据通过神经网络中的很多不同路径从输入节点流动到输出节点。只有一条路径是正确的，可将输入节点映射到正确的输出节点。为了找到这条路径，神经网络将使用反馈循环，其工作原理如下：

  1. 每个节点都会猜测该路径中的下一个节点。
  2. 它将检查猜测是否正确。节点将为引发更正确猜测的路径分配更高的权重值，而为引发不正确猜测的节点路径分配更低的权重值。
  3. 对于下一个数据点，节点将使用更高权重的路径进行新的预测，然后重复第 1 步。

卷积神经网络

卷积神经网络中的隐藏层执行特定的数学函数（如汇总或筛选），称为卷积。它们对于图像分类非常有用，因为它们可从图像中提取对图像识别和分类有用的相关特征。这种新形式更易于处理，而不会丢失对做出良好预测至关重要的特征。每个隐藏层提取和处理不同的图像特征，如边缘、颜色和深度。

损失函数

  • L2 Loss

\[ l(y, y') = 1/2(y-y')^{2} \]

  • L1 Loss

    \[ l(y, y') = |y-y'| \]

  • Huber's Robust Loss

    \[ l(y, y')=\left\{ \begin{gather*} |y-y'| - 1/2 && |y-y'|>1\\ 1/2(y-y')^{2} && else \end{gather*} \right. \]

激活函数

  • sigmoid σ

    \[ sigmoid(x) = \frac{1}{1+exp(-x)} \]

  • tanh 解决了 sigmoid 函数不易收敛的问题

    \[ tanh(x) = \frac{1-exp(-2x)}{1+exp(-2x)} \]

  • ReLU rectified linear unit 解决了 tanh 梯度消失的问题, 有稀疏性

    \[ ReLU(x) = max(x, 0) \]

神经网络结构

全连接层

全连接层是一种神经网络层，也叫做“密集层”。这种层在神经网络中的作用是将输入转换为输出。

在全连接层中，每个输入单元都与每个输出单元相连。这种连接方式使得全连接层能够学习高度非线性的模式。

全连接层通常用于深度学习模型中的分类和回归任务。

卷积层

平移不变性, 局部性

卷积层是一个特殊的全连接层

卷积层是神经网络中的一种常见层，主要用于图像处理任务。卷积层对输入数据进行卷积运算，并生成输出。

卷积层的输入是一个二维或三维张量，输出也是一个二维或三维张量。卷积层的参数包括卷积核（也称为滤波器）和偏差。卷积核是一个小的二维张量，它在输入数据上滑动，对输入进行卷积运算。

卷积层的主要作用是提取输入数据中的特征。例如，在图像分类任务中，卷积层可以学习到图像中的边缘、角点等特征。卷积层还可以减少输入数据的维度，并使用池化层来进一步降低数据维度。

核 kernel

池化层

类似卷积层, 比如最大池化层就是在 kernel 中找最大值, 平均池化层

池化层是神经网络中的一种常见层，主要用于图像处理任务。池化层对输入数据进行池化操作，并生成输出。

池化层的输入是一个二维或三维张量，输出也是一个二维或三维张量。池化层没有可学习的参数，它的作用主要是对输入数据进行降维和降采样。

池化层通常与卷积层一起使用，用于减小输入数据的维度和提取输入数据的重要特征。池化层还可以防止过拟合，并加速模型的训练过程。, 一般一个卷积层一个池化层, 卷积层的输出作为池化层的输入

归一化层

归一化层是一种神经网络层，它的作用是对输入数据进行归一化处理。归一化层通常用于图像处理任务中，可以帮助模型更好地收敛。

归一化层的输入是一个二维或三维张量，输出也是一个二维或三维张量。归一化层没有可学习的参数，它的作用是将输入数据的均值变为0，方差变为1。

例如，在使用归一化层对图像数据进行归一化处理时，可以将每个像素的值减去整个图像的均值，再除以整个图像的标准差。这样可以使得图像数据的值分布在0附近，有助于加速模型的训练。

归一化层通常与卷积层或全连接层一起使用，可以帮助模型更好地提取特征。

softmax回归

\[ \hat{y_{i}} = \frac{exp(o_{i})} {\sum_{k}exp(o_{k})} \]

输入为一维向量, 输出每个维度的概率

  1. 值变为非负
  2. 分母为 1
  3. 值为概率

使用交叉熵衡量预测和标号的区别

MLP多层感知机

单层感知机

\[ \begin{aligned} o=\sigma(<w,x>+b)\\ \sigma = \left\{ \begin{gather*} 1 && x>0\\ 0 && else \end{gather*} \right. \end{aligned} \]

initialize w = 0 and b = 0 
repeat
    if yi[<w, xi>+b] ≤ 0 \\分类错误
    then
      w<-w+yi xi and b<-b+yi; \\更新 w,x
  end if 
until all classified correctly

等价于批量为 1 的梯度下降

多层感知机

解决了 XOR 问题

隐藏层?

最典型的MLP包括包括三层：输入层、隐层(至少一个)和输出层，MLP神经网络不同层之间是全连接的（全连接的意思就是：上一层的任何一个神经元与下一层的所有神经元都有连接）。权重、偏置和激活函数

RNN

对于序列模型的神经网络

循环神经网络

o1  o2  o3  o4
|   |   |   |
h1->h2->h3->h4
    |   |   |
    x1  x2  x3  x4

相比 MLP, 多了对 ht-1的权重

梯度下降GD

\[ \begin{gather*} \theta \gets \theta - \varepsilon g\\ \varepsilon 学习率\\ g 梯度 \end{gather*} \]

随机梯度下降: SGD

每次随机抽取样本计算梯度

使用动量的随机梯度下降: 每次更新是给之前的梯度一个权重, 称之为动量

学习率 AdaGrad 算法

\[ \begin{gather*} r \gets r + g^{2}\\ \theta \gets \theta - \frac{\varepsilon}{\sqrt{r} + \delta}g\\ \delta 为一个小量,稳定数值计算 \end{gather*} \]

RMSProp 算法更新 r<-ρr+(1-ρ)g2

Adam 算法

L 损失函数

\[ \begin{gather*} g=\frac{1}{m}\nabla_{\theta}\sum^{m}_{i=1}L(f(x_{i}, \theta), y_{i})\\ s\gets\rho_{1}s+(1-\rho_{1})g\\ r\gets\rho_{2}r+(1-\rho_{2})g^{2}\\ \hat{s}\gets\frac{s}{1-\rho^{t}_{1}}\\ \hat{r}\gets\frac{r}{1-\rho^{t}_{}}\\ \theta \gets \theta - \frac{\varepsilon \hat{s}}{\sqrt{\hat{r}} + \delta}\\ \end{gather*} \]

反向传播bp

反向传播算法就是神经网中加速计算参数梯度值的算法

GNN

https://www.jianshu.com/p/5d3eaa1f5e20

DNN

深度神经网络

有时候也叫多层感知机

encoder decoder 架构

┌──────┐┌───┐┌──────┐
│never1││say││never2│
└┬─────┘└┬──┘└┬─────┘
┌▽───────▽────▽┐     
│encoder       │     
└┬───┬───┬─────┘     
┌▽─┐┌▽─┐┌▽─┐         
│v1││v2││v3│         
└┬─┘└┬─┘└┬─┘         
┌▽───▽───▽┐          
│input    │          
└┬────────┘          
┌▽──────────┐        
│decoder    │        
└───────────┘

attention 注意力机制

随意线索被称之为查询 (query)

每个输入是一个值(value) 和不随意线索 (key）的对

通过注意力池化层来有偏向性的选择选择某些输入

┌─────────┐┌───────────┐┌──────────┐ 
│x1       ││x2         ││x3        │ 
└┬───┬───┬┘└─┬────┬───┬┘└─┬───┬───┬┘ 
┌▽─┐┌▽─┐┌▽─┐┌▽──┐┌▽─┐┌▽─┐┌▽─┐┌▽─┐┌▽─┐
│q1││v1││k1││q2 ││k2││v2││k3││v3││q3│
└──┘└┬─┘└┬─┘└┬┬┬┘└┬─┘└┬─┘└┬─┘└┬─┘└──┘
     │   │  ┌│││──│───│───┘   │      
     │ ┌─│──││││──┘   │       │      
   ┌─│─│─│──│┘││      │       │      
┌──│─┘ │┌│──│─┘│   ┌──┘       │      
│  │┌──││┘  │ ┌┘   │┌─────────┘      
│┌─▽▽┐┌▽▽─┐┌▽─▽┐   ││                
││a21││a22││a23│   ││                
│└┬──┘└┬──┘└┬──┘   ││                
│┌▽────▽────▽──┐   ││                
││softmax      │   ││                
│└┬─────┬─────┬┘   ││                
│┌▽───┐┌▽───┐┌▽───┐││                
││a21'││a23'││a22'│││                
│└┬───┘└──┬─┘└┬───┘││                
│ │      ┌│───│────│┘                
│ │  ┌───││───│────┘                 
└┐│  │┌──││───┘                      
┌▽▽┐┌▽▽┐┌▽▽┐                         
│*1││*2││*3│                         
└┬─┘└┬─┘└┬─┘                         
┌▽───▽───▽┐                          
│    y    │                          
└─────────┘

transformer

使用encoder-decoder 架构

注意力机制+自循环

自循环体现在 decoder 将输出作为下一轮的输入, 同时在decoder 的 attention 中将未初始化向量的\(\alpha\)置为\(-\infty\) softmax后的\(\alpha' = 0\)

PyG

DGL

DyGNN

SGCN

线性代数

矩阵->每个列都是 基底, 每个矩阵代表了一种线性变换

复合变化: 从右往左

行列式的值: 线性变化后对应面积(体积)的变化

秩: 线性变换后的维数

点积: 投影的乘积

​ 列向量 点积 列向量 = 行向量 * 列向量

叉积: 向量组成的行列式的值(方向垂直)

线性方程组

1 2 3   x    1
0 1 2   y  = 1
2 3 4   z    1

1 2  x
0 1  y 这是一个从二维到三维的变换
2 3

\[ λ_{uv}=\frac{||h_u - h_v||_1}{d}, #(1) \]

systolic array