绪论

flowchart TD;
    数据元素--基本单位-->数据;
    数据项--组成 最小单位 -->数据元素;
    数据元素--集合-->数据对象;
    数据对象--子集-->数据;
    值的集合-->数据类型
    此集合上的操作-->数据类型
    数据元素--特定关系组成的集合-->数据结构

数据结构包括三方面的内容：逻辑结构、存储结构和数据的运算。

逻辑结构: 线性非线性

存储结构: 顺序存储, 链式存储, 索引存储, 散列存储

算法 5 个特性: 有穷性, 确定性, 可行性, 输入, 输出

栈、队列和数组

栈

卡特兰数: n 个不同元素进栈, 出栈元素不同排列的个数为

\[\frac{1}{n-1}C^{n}_{2n}\]

队列

front队头: 删除端

rear队尾: 插入端

循环队列

区分队空还是满: 一般牺牲一个单元来区分, 约定: 队头指针在队尾指针的下一位置作为队满的标志

栈在表达式求值中的应用

(3 + 4) × 5 - 6 就是中缀表达式 - × + 3 4 5 6 前缀表达式 3 4 + 5 × 6 - 后缀表达式

前缀表达式的计算机求值： 从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 op 次顶元素），并将结果入栈

中缀表达式到前缀表达式:

  1. 初始化两个栈：运算符栈S1和储存中间结果的栈S2；
  2. 从右至左扫描中缀表达式；
  3. 遇到操作数时，将其压入S2；
  4. 遇到运算符时，比较其与S1栈顶运算符的优先级： (4-1) 如果S1为空，或栈顶运算符为右括号“)”，则直接将此运算符入栈； (4-2) 否则，若优先级比栈顶运算符的较高或相等，也将运算符压入S1； (4-3) 否则，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；
  5. 遇到括号时： (5-1) 如果是右括号“)”，则直接压入S1； (5-2) 如果是左括号“(”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到右括号为止，此时将这一对括号丢弃；
  6. 重复步骤(2)至(5)，直到表达式的最左边；
  7. 将S1中剩余的运算符依次弹出并压入S2；
  8. 依次弹出S2中的元素并输出，结果即为中缀表达式对应的前缀表达式。

后缀表达式的计算机求值： 与前缀表达式类似，只是顺序是从左至右： 从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素 op 栈顶元素），并将结果入栈

将中缀表达式转换为后缀表达式：

  1. 初始化两个栈：运算符栈S1和储存中间结果的栈S2；
  2. 从左至右扫描中缀表达式；
  3. 遇到操作数时，将其压入S2；
  4. 遇到运算符时，比较其与S1栈顶运算符的优先级： (4-1) 如果S1为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈； (4-2) 否则，若优先级比栈顶运算符的高，也将运算符压入S1（注意转换为前缀表达式时是优先级较高或相同，而这里则不包括相同的情况）； (4-3) 否则，将S1栈顶的运算符弹出并压入到S2中，再次转到(4-1)与S1中新的栈顶运算符相比较；
  5. 遇到括号时： (5-1) 如果是左括号“(”，则直接压入S1； (5-2) 如果是右括号“)”，则依次弹出S1栈顶的运算符，并压入S2，直到遇到左括号为止，此时将这一对括号丢弃；
  6. 重复步骤(2)至(5)，直到表达式的最右边；
  7. 将S1中剩余的运算符依次弹出并压入S2；
  8. 依次弹出S2中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式（转换为前缀表达式时不用逆序）。

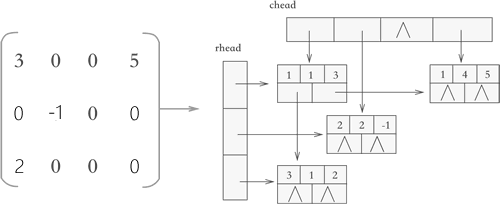
稀疏矩阵

三元组:(行标, 列表, 非零值)

十字链表法

img

KMP 算法.

举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"，我想知道，里面是否包含另一个字符串"ABCDABD"？并返回起始 index

右移位数 = 已匹配的字符数 - 对应的部分匹配值, 已匹配的字符数: 当前匹配失败字符之前的字符数; 对应的部分匹配值: 查表 匹配值: 前缀和后缀相同的字符数, 如abcda 的匹配值是1, abcab 的匹配数是 2 再将匹配值右移, 并以 -1 开始

pattern_char:  | a | b | c | d | a | b | a |
index:         | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
value:         | 0 | 0 | 0 | 0 | 1 | 2 | 1 |
the value means: The length of the longest proper prefix in the (sub)pattern that matches a proper suffix in the same (sub)pattern.
src_str: BBC ABCDAB ABCDABCDABDE
pattern      abcdaba
                 | ↑移动位数 = 已匹配的字符数 - 对应的部分匹配值=6-2=4
                 abcdaba
class Solution {
  public:
  //在 src 中找 pattern
    int strStr(string src_str, string pattern_str) {
        int src_length = src_str.length();
        int pattern_length = pattern_str.length();

        vector<int> next(pattern_length, 0);
        int i = 1, now = 0;
        while (i < pattern_length) {
            if (pattern_str[i] == pattern_str[now]) {
                now++;
                next[i] = now;
                i++;
            } else if (now != 0) {
                now = next[now - 1]; //根据之前的结果得到的
            } else {
                next[i] = 0;
                i++;
            }
        }

        int src_index = 0, pattern_index = 0;
        while (src_index < src_length) {
            if (src_str[src_index] == pattern_str[pattern_index]) {
                src_index++;
                pattern_index++;
            } else if (pattern_index != 0) {
                pattern_index = next[pattern_index - 1];
            } else {
                src_index++;
            }

            if(pattern_index == pattern_length)
                return src_index - pattern_index ;
        }
        return -1;
    }
};

树与二叉树

基本术语

结点的度: 一个结点的孩子的数量, 例如二叉树<=2

数的度: 树中结点的最大度数, 例如二叉树<=2

度>0 为分支结点, 度=0 为叶结点

结点的深度: 根结点深度为 1, 从根结点到叶结点累加

结点的高度: 从叶结点到根结点累加

树的高度: 树的最大层数

路径长度: 路径上经过的边的个数

平衡因子(Balance Factor, BF)是某个节点左子树和右子树的高度之差

\[树的结点数 =\sum{结点度数} +1\]

度为 m 的树第 i 层上至多有 \[m^{i-1}\]个结点

高度为 h 的 m 叉树至多有\[\frac{(m^{h}-1)}{m-1}\]个结点(\[S=m^{h-1}+m^{h-2}+...+m+1\])

具有n 个结点的 m 叉树的最小高度为\[\lceil log_m(n(m-1)+1) \rceil\] (取自前一结论)

二叉树的定义及其主要特性 (性质都要求递归)

满二叉树: 满的二叉树

完全二叉树: 满二叉树删去"倒数的几个节点"

二叉排序树: 左子树小于根节点, 右子树大于根节点

平衡二叉树: 树上任意节点的左右子树深度之差<=1

二叉树的性质

  • \[n_0 = n_2 +1\]
  • 完全二叉树从上到下, 从左到右, 从 1 到 n, 对于节点 i
    • \[parent = \lfloor\frac i 2\rfloor\]
    • \[leftchild = 2i\] , \[rightchild = 2i+1\]
    • \[depth = \lfloor log_2 i +1 \rfloor\]

二叉树的遍历

typedef int value_t;
class BiTree {
  public:
    BiTree* lchild;
    BiTree* rchild;
    value_t value;
};

void visit(BiTree* pt) {
    // cout value
}

void PreOrderRecur(BiTree* p_bitree) {
    if (p_bitree != nullptr) {
        visit(p_bitree);
        PreOrderRecur(p_bitree->lchild);
        PreOrderRecur(p_bitree->rchild);
    }
}

void PreOrderIt(BiTree* p_bitree) {
    BiTree* p = p_bitree;
    stack<BiTree*> s;
    while (!p || !s.empty()) {
        if (p) {
            visit(p);
            s.push(p);
            p = p->lchild;
        } else {
            p = s.top();
            s.pop();
            p = p->rchild;
        }
    }
}

void InOrderRecur(BiTree* p_bitree) {
    if (p_bitree != nullptr) {
        InOrderRecur(p_bitree->lchild);
        visit(p_bitree);
        InOrderRecur(p_bitree->rchild);
    }
}

void InOrderIt(BiTree* p_bitree) {
    BiTree* p = p_bitree;
    stack<BiTree*> s;
    while (!p || !s.empty()) {
        if (p) {
            s.push(p);
            p = p->lchild;
        } else {
            p = s.top();
            s.pop();
            visit(p);
            p = p->rchild;
        }
    }
}

void PostOrderRecur(BiTree* p_bitree) {
    if (p_bitree != nullptr) {
        PostOrderRecur(p_bitree->lchild);
        PostOrderRecur(p_bitree->rchild);
        visit(p_bitree);
    }
}


void PostOrderIt(BiTree* p_bitree) {
    BiTree* p = p_bitree;
    BiTree* recent_visited = nullptr;
    stack<BiTree*> s;
    while (!p || !s.empty()) {
        if (p) {
            s.push(p);
            p = p->lchild;
        } else {
            p = s.top();
            if (p->rchild && p->rchild != recent_visited) {
                p = p->rchild;
            } else {
                s.pop();
                visit(p);
                recent_visited = p;
                p = nullptr;
            }
        }
    }
}

void LevelOrder(BiTree* p_bitree) {
    BiTree* p = p_bitree;
    queue<BiTree*> q;
    q.push(p);
    while (!q.empty()) {
        p = q.front();
        q.pop();
        visit(p);
        if(p->lchild)
            q.push(p->lchild);
        if(p->rchild)
            q.push(p->rchild);
    }
}

根据遍历结果构造二叉树

IMG_9CD10B97876E-1

线索二叉树

规定: 若无左子树, lchild 指向前驱节点, 若无右子树, rchild 指向后继节点, ltag=1 代表前驱, rtag=1 代表后继 根据遍历方式可分为前序中序后序线索二叉树

class ThreadBiTree {
  public:
    ThreadBiTree* lchild;
    ThreadBiTree* rchild;
    bool ltag;
    bool rtag;
    value_t value;
};

void visit(ThreadBiTree* p) {}

void InThread(ThreadBiTree* p, ThreadBiTree* pre) {
    if (p != nullptr) {
        InThread(p->lchild, pre);
        if (p->lchild == nullptr) {
            p->lchild = pre;
            p->ltag = true;
        }
        if (pre != nullptr && pre->rchild == nullptr) {
            pre->rchild = p;
            pre->rtag = true;
        }
        pre = p;
        InThread(p->rchild, pre);
    }
}

void CreateInThread(ThreadBiTree* t) {
    ThreadBiTree* pre = nullptr;
    if (t != nullptr) {
        InThread(t, pre);
        pre->rchild = nullptr;
        pre->rtag = 1;
    }
}

ThreadBiTree* FirstNode(ThreadBiTree* p) {
    while (p->ltag == false)
        p = p->lchild;
    return p;
}

ThreadBiTree* NextNode(ThreadBiTree* p) {
    if (p->rtag == false)
        return FirstNode(p->rchild);
    else
        return p->rchild;
}

void InOrderThread(ThreadBiTree* t) {
    for (ThreadBiTree* p = FirstNode(t); p != nullptr; p = NextNode(p))
        visit(p);
}

树、森林

双亲表示法

typedef struct{
  ElemType data;
  int parent
} OTNode;
//root's parent = -1
typedef struct{
  PNTNode nodes[MAX_SIZE];
  int n;
}PTree;

孩子表示法

┌─┬─┐    ┌─┐     ┌─┐        
│0│R│───▶│1│────▶│2│        
│1│A│    └─┘     └─┘        
│2│B│                       
│3│C│    ┌─┐                
│4│D│───▶│6│                
│5│E│    └─┘                
│6│F│                       
└───┘

孩子兄弟表示法(二叉树表示法)

typedef struct CSNode{
  ElemType data;
  struct CSNode * firstchild, *nextsibling;
} CSNode, *CSTree;
//nextsibling 是本节点的兄弟节点的指针

树、森林与二叉树的转换

树->二叉树(唯一)

每个节点左指针指向第一个孩子, 右指针指向本节点相邻的右兄弟(左孩子右兄弟)

森林->二叉树(唯一)

现将每棵树转换为二叉树, 将树的根节点彼此视为兄弟连接到右指针上(从树->二叉树时, 根节点的右必为空)

树和森林的遍历

树遍历

  • 先根遍历, 先访问根节点,再访问每棵子树, 类似对应二叉树的先序遍历
  • 后根遍历, 先遍历子树再访问根节点, 类似对应二叉树的中序遍历

森林遍历

  • 先序遍历, 先访问根节点,再访问每棵子树, 类似对应二叉树的先序遍历
  • 中序遍历(也叫后序遍历), 先遍历子树再访问根节点, 类似对应二叉树的中序遍历

哈夫曼树和哈夫曼编码

带权路径长度

\[WPL = \sum_{i=1}^{n}{w_il_i}\]

\(w_i\)为第 i 叶节点的权值, \(l_i\)为该叶节点到根节点的路径长度

WPL 最小的二叉树称为哈夫曼树(最优二叉树)

构造哈夫曼树

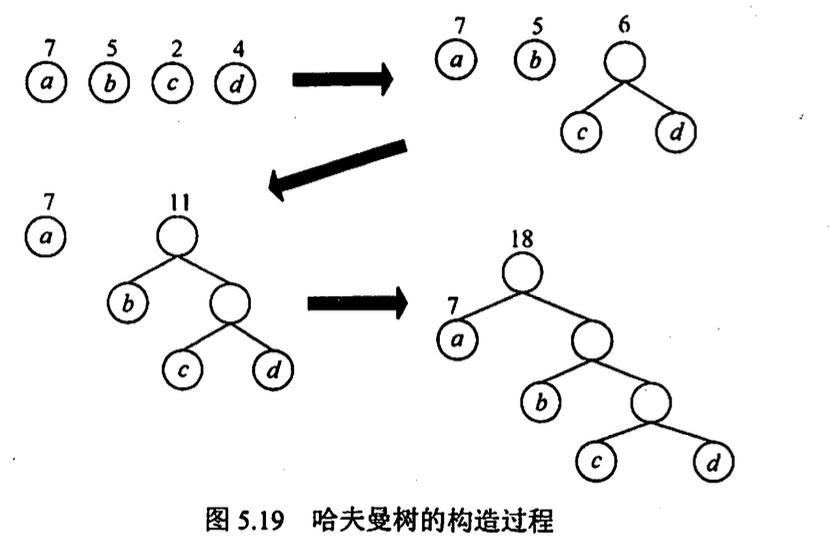
截屏2023-05-22 14.23.47

哈夫曼编码是一种可变长度编码, 使用频率越高长度越短

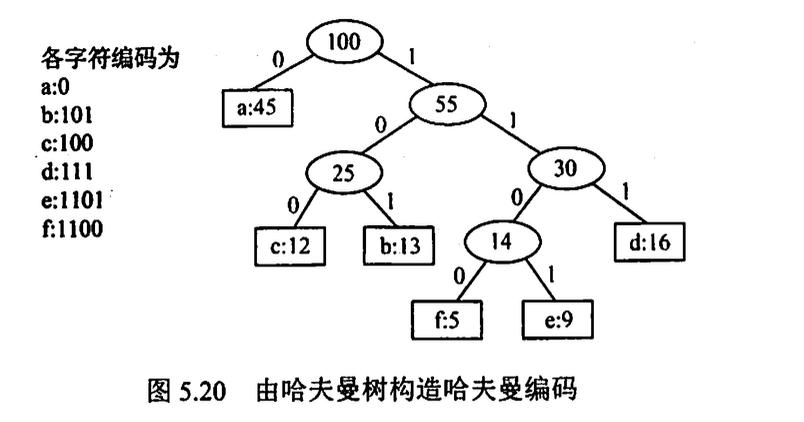
截屏2023-05-22 14.25.26

哈夫曼树不一定唯一(左右子树是 0 或 1 不规定; 有相同权值的节点. 但所有哈夫曼树最后的 WPL 是相同的)

并查集

并查集的思想是用一个数组表示了整片森林（parent），树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

图

图的定义

简单图: 如果图满足: 不存在重复边, 不存在顶点到自身的边

完全图: 每两个顶点之间都存在边(有向图则需要两条边) \(E = \frac{n(n-1)}{2}\)

子图: 顶点和边都是子集

生成子图: 顶点相同, 边是子集

连通图: 无向图中任意顶点都是连通的, 无向图中的极大连通子图称为连通分量

强连通图: 有向图中任意中任意顶点都是连通的, 有向图中的极大强连通子图称为连通分量

生成树: 连通图的生成树是包含全部顶点的一个极小连通子图, 对生成树而言, 去掉一条边就会变成非连通图, 加上一条边就会出现回路

生成森林: 非连通图中连通分量的生成树构成了飞连通图的生成森林

带权图又称网

稀疏图稠密图: 当满足\(|E|<|V|log|V|\) 可视为稀疏图

路径长度: 路径上边的个数

简单路径: 顶点不重复出现的路径

距离: 最短路径的长度

有向树: 一个顶点入度=0, 其余顶点入度=1 的有向图称为有向树

图的存储

邻接矩阵法

#define MaxVertexNum 100
typedef int EdgeType;
typedef char VertexType;
typedef struct {
    VertexType vex[MaxVertexNum];
    EdgeType edge[MaxVertexNum][MaxVertexNum];
    int vexnum, arcnum;
} MGraph;

适用于稠密图

无向图只需存储三角矩阵的元素

\(A^n\)的元素\(A^n[i][j]\)等于从 i 到 j 顶点长度为 n 的路径的数量

难以数出边的数量

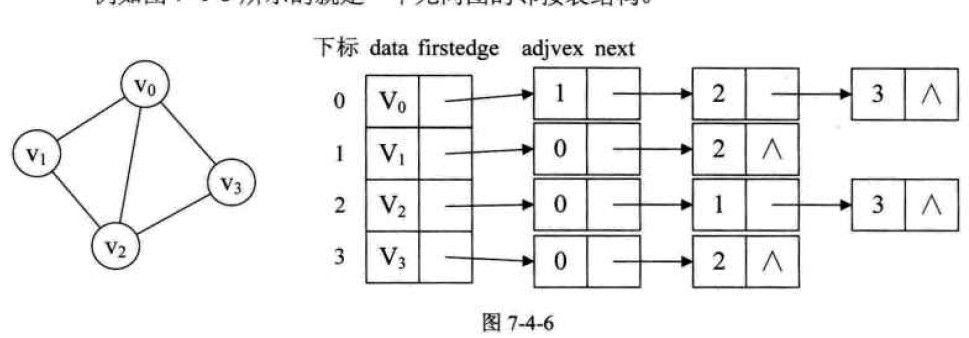
邻接表法

#define MaxVertexNum 100
typedef int EdgeType;
typedef char VertexType;

typedef struct ArcNode {
    int adjvex;
    struct ArcNode* next;
    // EdgeType weight
} ArcNode;

typedef struct VNode {
    VertexType data;
    ArcNode* first;
} VNode, AdjList[MaxVertexNum];

typedef struct {
    AdjList vertices;
    int vexnum, arcnum;
} ALGraph;

无向图的存储中会有重复

难以判断两顶点之间是否存在边

有向图存储的是出度边, 难以数出入度

邻接表不唯一

img

img

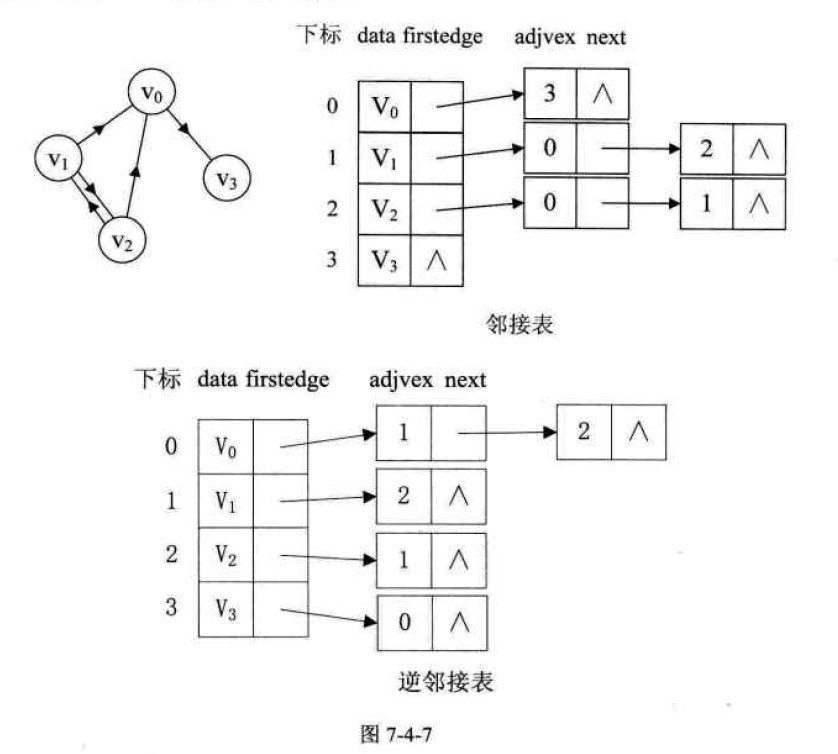
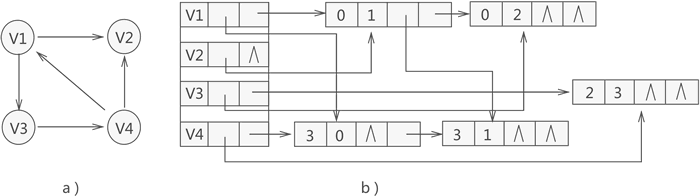
十字链表(有向图)

typedef struct ArcNode{
  int tailvex;//弧头顶点编号
  int headvex;//弧尾顶点编号
  ArcNode* hlink;//弧头相同的下一个弧节点
  ArcNode* tlink;//弧尾相同的下一个弧节点
  Data info;
} ArcNode;

typedef struct VexNode{
  Data data;
  ArcNode* firstin;//以本顶点为弧头的第一个弧
  ArcNode* firstout;//以本顶点为弧尾的第一个弧
}
十字链表存储有向图示意图

邻接多重表(无向图)

typedef struct ArcNode{
  int ivex;//顶点编号
  int jvex;//顶点编号
  ArcNode* ilink;//ivex相同的下一个弧节点
  ArcNode* jlink;//jvex相同的下一个弧节点
  Data info;
} ArcNode;

typedef struct VexNode{
  Data data;
  ArcNode* firstedge//第一条边
}

图的遍历

广度优先搜索 BFS

别混合 dfs, bfs 是一层一层的

vector<bool> visited(MAX, false);
queue<DataType> q;
void BFS(Graph g, int v){
    visit(v);
    visited[v] = true;
    q.push(v);
    while(!q.empty()){
        v = q.front();
        q.pop();
        for(int w = FirstNeighbor(g, v); w>=0; w = NextNeighbor(g, v, w))
        if(!visited[w]){
            visit(w);
            visited[w] = true;
            q.push(w);
        }
    }
}

void BFSTraverse(Graph g){
    for(int i=0; i<g; i++)
        if(!visited[i])
            BFS(g, i);
}

空间复杂度: S(V)

邻接表时间复杂度: O(V+E)

邻接矩阵时间复杂度: O(V2)

BFS求单源最短路径

#define Max_Distance 10e9
void BFSminDistance(Graph g, int u){
    vector<int> distance(max_vex_count, Max_Distance);
    vector<bool> visited(max_vex_count, false);
    visited[u] = true;
    distance[u] = 0;
    queue<int> q;
    q.push(u);
    while(!q.empty()){
        u = q.front();
        q.pop();
        for(int w = FirstNeighbor(g, u); w>=0; w = NextNeighbor(g, u, w))
        if(!visited[w]){
            visited[w] = true;
            distance[w] = distance[u] + 1;
            q.push(w);
        }
    }
}

深度优先搜索 DFS

vector<bool> visited(MAX, false);
void DFS(Graph g, int v) {
    visit(v);
    visited[v] = true;
    for (int w = FirstNeighbor(g, v); w >= 0; w = NextNeighbor(g, v, w))
        if (!visited[w]) {
            DFS(g, w);
        }
}

void DFSTraverse(Graph g) {
    for (int i = 0; i < g; i++)
        if (!visited[i])
            DFS(g, i);
}

空间复杂度: S(V) 运行栈

邻接表时间复杂度: O(V+E)

邻接矩阵时间复杂度: O(V2)

最小生成树

边的权值之和最小的生成树称为最小生成树

当各边权值不相等时, 最小生成树唯一, 树的最小生成树是自己本身 1.对图中的每一条边，扫描其他边，如果存在相同权值的边，则对此边做标记。 2.然后使用Kruskal（或者prim）算法求出最小生成树。 3.如果这时候的最小生成树没有包含未被标记的边，即可判定最小生成树唯一。 如果包含了标记的边，那么依次去掉这些边，再求最小生成树，如果求得的最小生成树的权值和原来的最小生成树的权值相同，即可判断最小生成树不唯一。

最小生成树的边数=顶点数-1

  • 通用方法

    从∅开始, 加入权重最小的边, 且保证不出现回路
    get_min_generate_tree(g)
    	tree = null
    	while tree isnot generate_tree
    		do:
    			找到一条权重最小边(u, v),
          并且加入 tree 后无回路
    			tree = tree+(u, v)

  • Prim 算法

    从∅开始,加入权重最小的边, 边的一个顶点是已收入集合的, 一个顶点是未收入集合的
    Prim(g, tree)
    	tree = null
    	V_tree = {w} # any vertex as w
    	while V-V_tree != null:
    		find (u, v)where:
          u isin V_tree, 
          v isin V-V_tree, 
          and (u, v) is min
    		Tree = Tree + (u, v)
    		V_tree = V_tree + v

    O(V2)

  • Kruskal 算法

    从∅开始, 初始认为每个顶点为一棵单独的树, 加入权重最小的边及其两个顶点, 边的两个顶点分别属于不同的连通分量
    Kruskal(V, tree)
    	tree = V
    	# connected component 连通分量
    	connect_cp_count = n
    	while connect_cp > 1:
    		find min(u, v) in E
    		if u, v isin different conncted component:
    			tree = tree + (u, v)
    			connect_cp_count--

dijkstra 算法 单源

邻接矩阵时间复杂度: O(V2)

邻接表时间复杂度: O(V2)

有边权值为负时, 不适用

从只有出发点的集合开始,加入距离最近的点,将集合整体看做一个点,更新到集合外点的距离
//有 n 个网络节点，标记为 1 到 n。
//给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。
//现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。
#include <vector>
using namespace std;
class Solution {
  public:
    int
    dijkstra(vector<vector<int>>& adj_matrix, int vertex_cnt, int src_vertex) {
        const int inf = INT_MAX / 2;
        vector<vector<int>> g(vertex_cnt, vector<int>(vertex_cnt, inf));
        for (auto& t : adj_matrix) {
            int x = t[0] - 1, y = t[1] - 1;
            g[x][y] = t[2];
        } // 邻接表转换到邻接矩阵

        vector<int> dist(vertex_cnt, inf);
      	src_vertex--;//as index
        dist[src_vertex] = 0;
        vector<bool> used(vertex_cnt, false);

        for (int i = 0; i < vertex_cnt; ++i) {
            int x = -1;
            for (int y = 0; y < vertex_cnt; ++y) {
                if (used[y]==false && (x == -1 || dist[y] < dist[x])) {
                    x = y;
                }
            }
            used[x] = true;
            for (int y = 0; y < vertex_cnt; ++y) {
                dist[y] = min(dist[y], dist[x] + g[x][y]);
            }
        }

        int ans = *max_element(dist.begin(), dist.end());
        return ans == inf ? -1 : ans;
    }
};

floyd 算法 多源

\(A^k[i][j] = Min\{A^{k-1}[i][j], A^{k-1}[i][k] + A^{k-1}[k][j]\}\)

循环 n 次(n 为顶点数)

private void floyd() {
    for (int k = 0; k < n; k++) {//循环 n 次
        //对所有 Aij
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                a[i][j] = Math.min(a[i][j], a[i][k] + a[k][j]); //核心
            }
        }
    }
}

拓扑排序

AOV 网(Activity on Vertex Network) 有向边<Vi, Vj>表示 i 活动优先于 j 活动

拓扑排序(拓扑序列): 在有向无环图中, 每个顶点只出现一次, A 在 B 前则不存在从 B 到 A 的路径( 步骤:

  • 从 AOV 中选择一个没有前驱的顶点并输出
  • 删除该顶点和所有以它为起点的有向边
  • 重复 1, 2 直到 AOV 为空

邻接表时间复杂度: O(V+E)

邻接矩阵时间复杂度: O(V2)

关键路径

AOE 网(Activity On Edge Network), 顶点表示事件, 边表示活动, 边上的权值表示活动开销

AOE 网只有一个入度=0 的点, 一个出度=0 的点

AOE 网中的最长路径为关键路径, 关键路径上的点叫做关键活动

  • 事件 vk的最早发生时间 ve(k) ve(源点) = 0 \(ve(k) = Max\{ ve(j)+Weight(v_j, v_k) \}\) 其中 k 为 j 的任意后继 计算 ve 从源点开始从前向后
  • 事件 vk的最迟发生时间 vl(k) vl(汇点) = ve(汇点) \(vl(k) = Min\{ vl(j)-Weight(v_k, v_j) \}\) 其中 k 为 j 的任意前驱 计算 ve 从汇点开始从后向前
  • 活动 ai最早开始时间 e(i) = ve(k), 其中<vk, vj>表示活动 ai
  • 活动 ai最迟开始时间 l(i) = vl(j) - Weight(vk, vj), 其中<vk, vj>表示活动 ai
  • 活动 ai最早开始时间与最迟开始时间差额 d(i) = l(i) - e(i), 即时间余量

AOE 网算法:

  1. 从源点除法算 ve(事件 vk的最早发生时间)
  2. 从汇点出发算 vl(事件 vk的最迟发生时间)
  3. 根据 ve 求 e (活动 ai最早开始时间)
  4. 根据 vl 求 l (活动 ai最迟开始时间)
  5. 根据e, l 求 d, 所有 d=0 的活动构成关键路径

查找

平均查找长度 \(ASL = \sum^n_{i=1}P_iC_i\)

Pi为查找概率, 一般认为是 1/n, Ci是需要进行比较的次数

顺序查找

利用哨兵减少判断语句

  1. 一般线性表: 遍历

    \(ASL_{success} = \sum^n_{i=1}\frac1n(n-i+1) = \frac{n+1}2\)

    \(ASL_{failed} = n+1\)

  2. 有序表顺序查找

    判定树

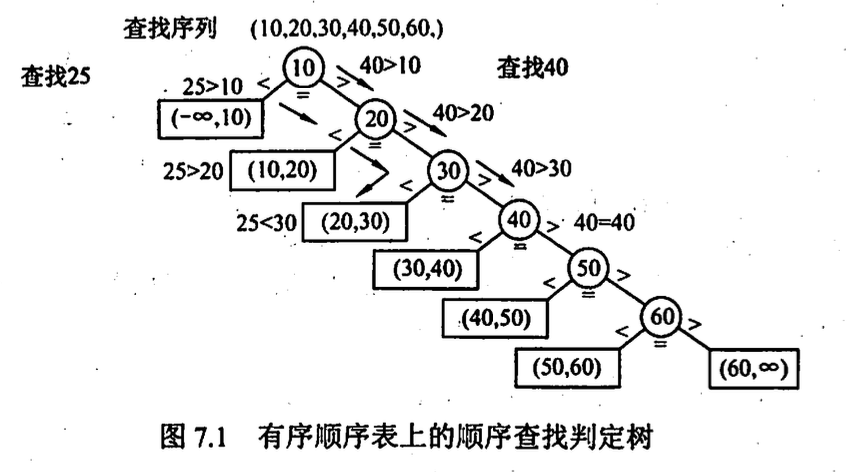
    截屏2023-05-26 09.50.09

    \(ASL_{success} = \sum^n_{i=1}\frac1n(n-i+1) = \frac{n+1}2\)

    \(ASL_{failed} = \sum^n_{i=1}q_i(l_i-1) = \frac{1+2+...+n+n}{n+1} = \frac n2 + \frac n{n+1}\)

    qi为失败概率, li为节点层数

折半查找 (二分查找, 有限顺序表)

typedef int elemtype;
int BinarySearch(vector<elemtype> vec, elemtype key) {
    int low = 0, high = vec.size(), mid = 0;
    while (low <= high) {
        mid = (low + high) / 2;
        if (vec.at(mid) == key)
            return mid;
        else if (vec.at(mid) > key)
            high = mid - 1;
        else
            low = mid + 1;
    }
    return -1;
}

判定树(平衡二叉树)

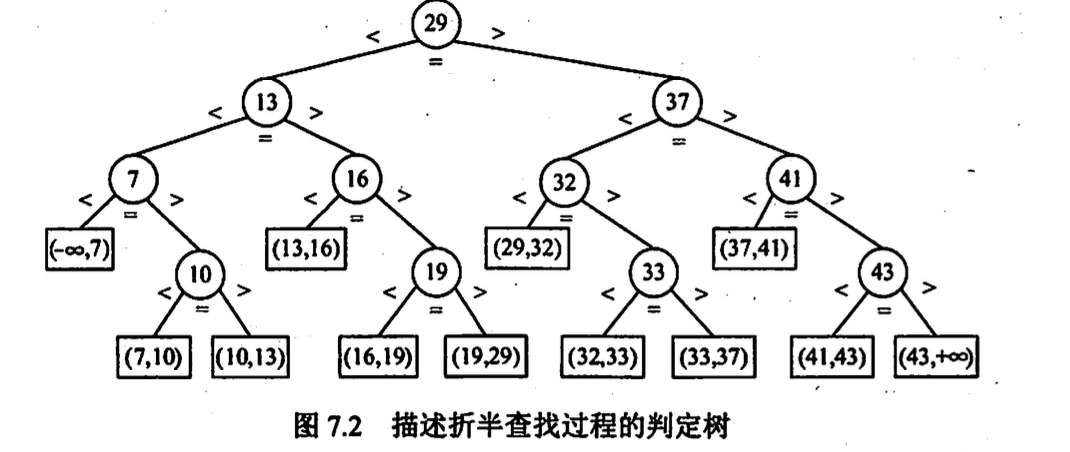
截屏2023-05-26 13.03.34

$ASL_{success} = 1n ^n_{i=1}l_i $

$= 1n(11+22+43+...+h2^{h-1}) $

$= n log_2(n+1) - 1 $

\(\approx log_2(n+1) -1\)

查找成功, 次数为层数;

查找失败, 次数为叶节点层数+1(两种情况, 如 6, 9 分别对应 3, 4 次比较)

分块查找

将顺序表通过取关键字切分为多个块, 块之间有序, 块内无序

\(ASL = L_I + L_S = \frac{b+1}2 + \frac{s+1}2 = \frac {s^2+bs+2s}{2s} = \frac{s^2 + n + 2s}{2s}\)

当 \(s = \sqrt n\) 时有最小值 \(\sqrt{n+1}\)

二叉排序树 (BST) (搜索树, 查找树)

提高增删改查速度

定义: 左子树上所有结点 < 根节点, 右子树上所有结点 > 根节点, 左右子树也是二叉排序树

对其进行中序遍历可以得到一个递增的有序序列

给定初始值序列, 二叉排序树唯一, 只给定初始值不给序列, 二叉排序树不唯一

node* BSTSearch(node* root, elemtype key) {
    while (root != nullptr && key != root->data) {
        if (key < root->data)
            root = root->lchild;
        else
            root = root->rchild;
    }
    return root;
}
elemtype BSTInsert(node* root, elemtype data) {
    if (root == nullptr) {
        root = new node();
        root->data = data;
        root->lchild = nullptr;
        root->rchild = nullptr;
        return 1;
    } else if (data == root->data) {
        return 0;
    } else if (data < root->data) {
        return BSTInsert(root->lchild, data);
    } else {
        return BSTInsert(root, data);//?rchild
    }
}
void CreateBST(node* root, elemtype datas[], int data_length) {
    int i = 0;
    while (i < data_length) {
        BSTInsert(root, datas[i]);
        i++;
    }
}

删除: 左子树或者右子树为空: 用另一个子树替代

左右子树均不为空: 令要删除的节点的直接后继(直接前驱)(中序)替代, 删除该后继, 之后重复

\(ASL = O(log_2n)\)

当使用有序序列构造时获得最差情况单枝树, ASL = O(n)

平衡二叉树 AVL 树(Adelson-Velsky and Landis Tree)

定义: 任意节点左右子树高度差 <= 1

平衡二叉树插入: 插入节点后调整平衡 找第一个不平衡节点

  1. LL A 的左子树的左子树上插入 截屏2023-05-26 13.45.18
  2. RR 同上
  3. LR A 的左子树的右子树上插入 截屏2023-05-26 13.46.16
  4. RL 同上

平衡二叉树删除: 删除后调整, 从叶到根层层调整(可能调整多次)

红黑树

定义:

  1. 每个节点是红或黑, 根节点和叶节点为黑(空节点被视为叶节点)
  2. 不存在相邻红节点
  3. 对每个节点, 从该节点到任意叶节点的简单路径上的黑节点数量相同, 其数量叫做黑高 bh, 根节点的黑高为树的黑高

红黑树的插入

  1. 按照二叉排序树方法插入节点z, 并着红色, 如果父节点是黑色则插入完毕
  2. 如果z 是根节点, 着黑色, 插入完毕
  3. 如果 z 父节点是红色, 类似平衡二叉树
    1. z 叔节点 y 是黑色, z 是右孩子 LR
    2. z 叔节点 y 是黑色, z 是左孩子 LL
    3. z 父节点和叔节点都红 将父节点和叔节点变黑, 爷节点变红, 将爷节点视为插入节点, 重复

红黑树的删除 ?

  1. 按二叉排序树方法删除
  2. 删除节点如果只有左或右子树, 直接删除并变色
  3. 删除节点为红且没有孩子, 直接删除
  4. 删除节点y为黑且没有孩子, 寻找空节点 x 替代, 视 x 为双重黑节点
    1. x 的兄弟节点 w 为红, 对 w 做 L(左旋) 操作, 转换到情况 2, 3, 4
    2. x 兄弟节点 w 为黑, w 右孩子为红 RR, 对 w L
    3. x 兄弟节点 w 为黑, w 左孩子为红, 右孩子为黑, 对 w R, 回到情况 2
    4. x 兄弟节点w 为黑, w 左右孩子都为黑, 将 w 变红, x.p 变黑

B树和B+树

eg: 用磁盘数据库, 需要索引(key=index, value=pointer to sector) 索引过大时需要索引的索引, 因此需要 b 树

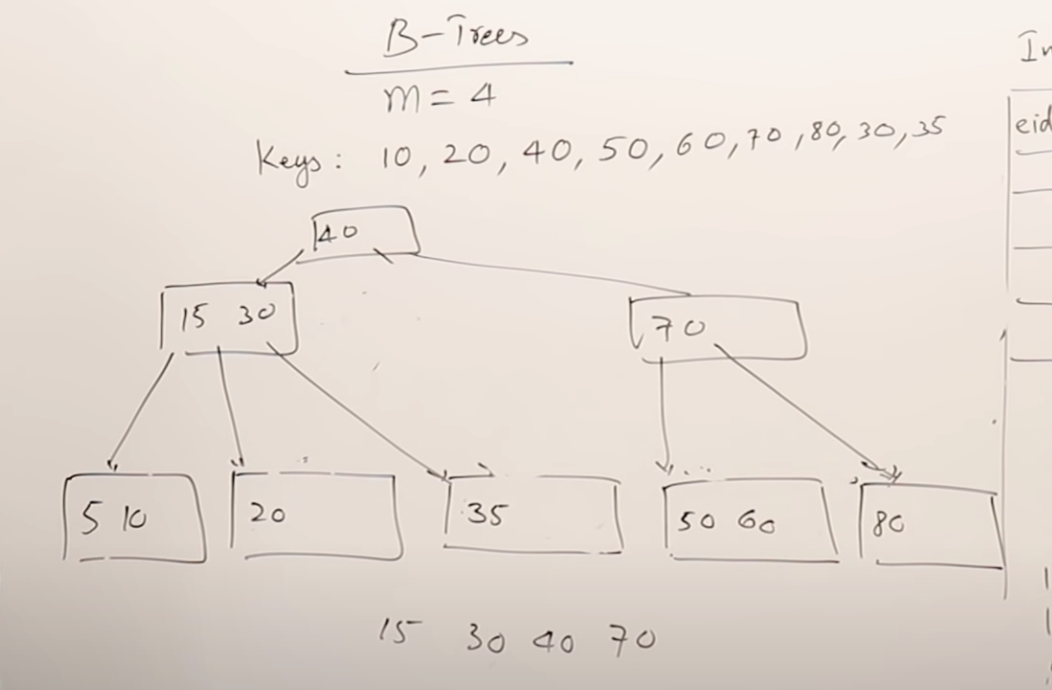
image-20231115202120990

B树(B-树)及其基本操作

m 阶 B 树为所有结点平衡因子都为 0 的 m 路平衡查找树

定义:

  1. 每个节点至多有 m 棵子树

  2. 除根节点外所有非叶节点至少有\(\lceil \frac m2 \rceil\)棵子树

  3. 非叶节点结构如下 

    ┌──────────────────────────┐ 
    │n p0 k1 p1 k2 p2 ... kn pn│ 
    └──────────────────────────┘ 
    k 为关键字(已升序排序), p 为子树指针, n 为关键字数量
    每个内部节点的每个关键字都都带有数据

  4. 所有叶节点(外部节点, 空节点)在同一层且不带信息, 即指向叶节点的指针是空指针

  5. b 树的高度一般不包括叶节点

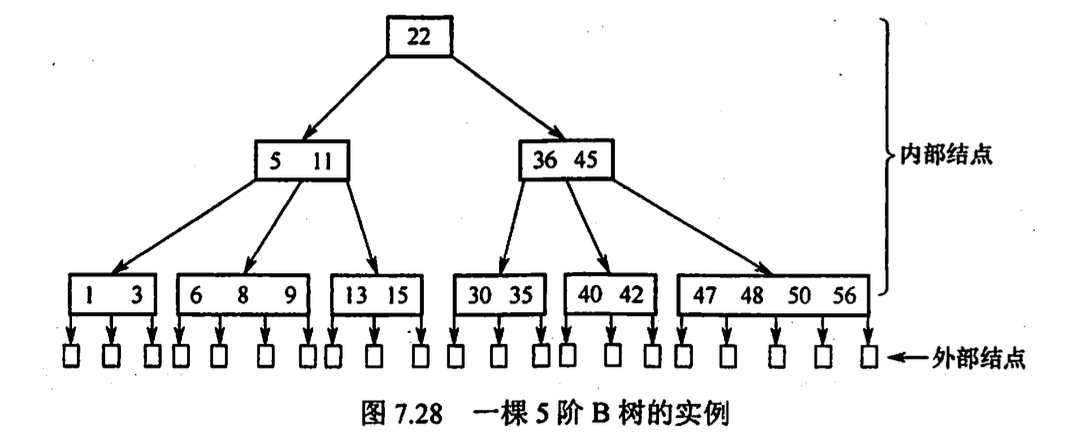
截屏2023-05-26 15.51.26

B 树高度(不包含最后一层空指针(有无都可?))

  • 高度为 h 的有 n 个关键字的 m 阶 B 树:

    ​ $n(m-1)(1+m+m2+m3 + ... + m^{h-1}) = m^h-1 $

  • 对于关键字数为 n 的 B 树, 最后一层空节点的个数为 n+1

    \(n+1\geq 2(\lceil \frac m2 \rceil)^{h-1}\)

B 树插入关键字k

  1. 寻找倒数第一层非空节点(即寻找插入位置)
  2. 如果插入后关键字数<m-1 直接插入, 否则对节点进行分裂
  3. 从中间位置(\(\lceil \frac m 2 \rceil\))分割, 左边保留在原结点, 右边进入新节点, 中间关键字进入父节点, 若父节点关键字超出, 重复此操作

B 树删除关键字 k

  1. 对于不是最底层非叶结点的关键字, 可以用 k 的前驱(后继)k'替代 k, 直到 k'落入最底层非叶结点
  2. 在终端节点中: 若关键字个数>=\(\lceil \frac m2 \rceil\), 可以直接删除
  3. 在终端节点中: 若关键字个数<\(\lceil \frac m2 \rceil\), 且兄弟可借, 则调整父节点与兄弟节点
  4. 若兄弟不够借, 则删除后与兄弟节点合并, 此时父结点内关键字会减少, 重复此过程直到符合 b 树要求

B+树的基本概念

  1. 每个节点至多有 m 棵子树,
  2. 除根节点外所有非叶节点至少有\(\lceil \frac m2 \rceil\)棵子树
  3. 节点子树个数与关键字数相同
  4. 所有叶节点包含全部关键字和指向其记录(数据)的指针, 叶节点中关键字排序, 相邻叶节点相互链接
  5. 分支节点中仅包含它各个子节点中关键字的最大值及其指针
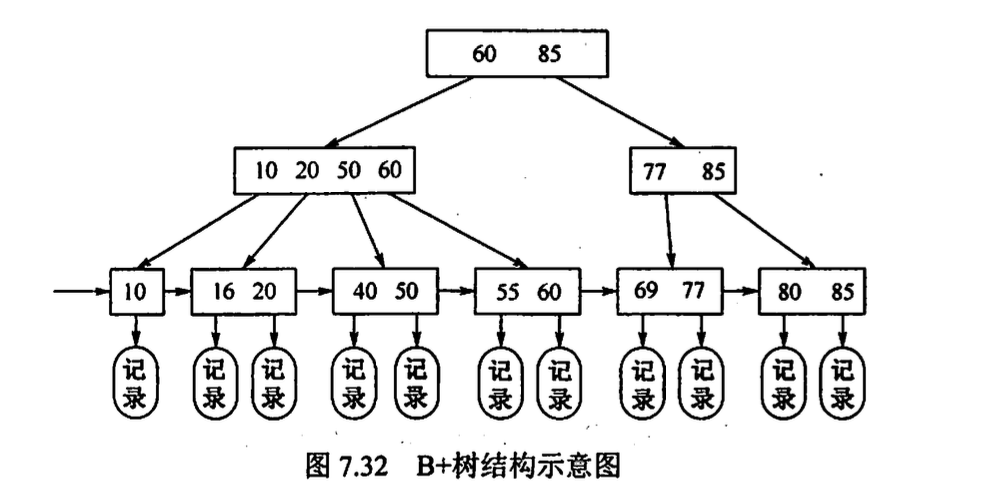
截屏2023-05-26 15.53.25

B*树

是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针

B树定义了非叶子结点元素个数至少为(2/3)M，即块的最低使用率为2/3（代替B+树的1/2）

B*的查询、插入和删除操作和B+树差不多

只不过会遵循非叶子结点元素个数至少为(2/3)*M的特点

比如，对于3阶B*树，当元素个数大于1的时候

每个非叶子节点的元素个数，至少为两个

散列表

散列函数: hash(key) = addr

散列表: 根据关键字直接进行访问的数据结构, 是一种直接映射

装填因子 \(\alpha = \frac{散列表中记录数 n}{散列表总长度 m}\) 即散列表装满的程度, α越大装的越满

散列函数的构造方法

  1. 直接定址法

    h(key) = a*key +b

  2. 除留余数法

    h(key) = key%p

  3. 数字分析法

    对关键字进行分析, 考察分布均匀程度

  4. 平方取中法

    取关键字的中间几位作为散列地址

处理冲突的方法

  1. 开放定址法

    \(h_i = [h(key)+d_i]\%m\)

    m为散列表长, di为增量序列

    注: 不能随便删除元素, 需要标记后定期维护

    1. 线性探测法: di = 0, 1, 2 ... m-1 这样可能会争夺正常映射的散列表位置
    2. 平方探测法(二次探测法): \(d_i = 0^2, 1^2, (-1)^2, 2^2...k^2, (-k)^2\) k<=m/2, 散列表长度 m 必须是一个可以表示成 4k+3 (?)的素数(如此可以保证, 只要散列表中有一半空元素, 就一定能插入)
    3. 双散列法\(d_i = h_2(key)\): \(h_i=[h(key)+i*h_2(key)]\%m\) i为冲突次数
    4. 伪随机序列法: di = 伪随机序列

  2. 拉链法: 存储在线性链表中

排序

插入排序

寻找第一个未排序的元素, 将未排序的元素插入已排序的前端序列

vector<int> sortArray(vector<int>& nums) {
    int sorted_idx = 0;
    int guard = nums[0];
    for (int unsorted_idx = 1; unsorted_idx < nums.size(); unsorted_idx++) {
        sorted_idx = unsorted_idx - 1;
        guard = nums[unsorted_idx];
        int i = sorted_idx;
        for (; i >= 0 && nums[i] > guard; i--) {
            nums[i + 1] = nums[i];
        }
        nums[i+1] = guard;
    }
    return nums;
}

空间复杂度: S(1)

时间复杂度: 最好(有序)O(n), 最坏(逆序)O(n2), 平均: 比较次数=移动次数=\(\frac{n^2}4\)

从后向前比较移动时: 稳定

折半插入排序

对有序序列进行二分查找

void HalfInsertSort(ElemType list[], int length) {
    int unsorted_index, sorted_index, low, high, mid, find_insert;
    ElemType guard;
    for (unsorted_index = 1; unsorted_index < length; unsorted_index++) {
        sorted_index = unsorted_index - 1;
        low = 0;
        high = sorted_index;
        guard = list[unsorted_index];
        while (low <= high) {
            mid = (low + high) / 2;
            if (list[mid] > guard)
                high = mid - 1;
            else
                low = mid + 1;
        }
        // list[high]<=guard<list[high+1], 插入位置: high+1
        for (find_insert = sorted_index; find_insert >= high + 1;
             find_insert--) {
            list[find_insert + 1] = list[find_insert];
        }
        list[find_insert + 1] = guard;
    }
}

平均时间复杂度: 比较次数 = nlog2n, 移动次数 = n2/4

稳定

希尔排序(缩小增量排序)

以 gap 分组为 length/gap 个组, 每个组(跳跃间隔)各自排序, gap 逐渐缩小到 1

void ShellSort(int list[], int length) {
    int gap, for_each_group, i;
    for(gap = length/2; gap > 0; gap /= 2)
        for(for_each_group = gap; for_each_group < length; for_each_group++)
            for(i = for_each_group - gap; i >= 0 && list[i] > list[i+gap]; i -= gap) {
                swap(list[i], list[i+gap]);//直接插入排序
            }
}

空间复杂度: 1

时间复杂度: 约为 n1.3, 最坏 n2

不稳定

冒泡排序

每次排序将未排序序列中最大的元素移到未排序序列最后, 但是两两比较

// 普通冒泡排序
void BubbleSort(ElemType list[], int length) {
    for (int for_each = 0; for_each < length; for_each++) {
        int sorted_index = length - for_each;
        for (int unsorted_index = 0; unsorted_index < sorted_index - 1;
             unsorted_index++) {
            if (list[unsorted_index] > list[unsorted_index + 1]) {
                swap(list[unsorted_index], list[unsorted_index + 1]);
            }
        }
    }
}
// 改进冒泡排序, 最好情况 O(n) = n-1
void BubbleSort(ElemType list[], int length) {
    bool didSwap;
    for (int for_each = 0; for_each < length; for_each++) {
        didSwap = false;//如果在某次遍历发现没有交换说明已排序完
        int sorted_index = length - for_each;
        for (int unsorted_index = 0; unsorted_index < sorted_index - 1;
             unsorted_index++) {
            if (list[unsorted_index] > list[unsorted_index + 1]) {
                swap(list[unsorted_index], list[unsorted_index + 1]);
                didSwap = true;
            }
        }
        if (didSwap == false)
            return;
    }
}

空间复杂度: 1

时间复杂度: 最好(顺序) n-1. 最坏(逆序): 比较次数:\(\frac{n(n-1)}2\), 移动次数: \(\frac{3n(n-1)}2\) (3是 swap 函数的时间复杂度)

稳定

快速排序

一次确定一个元素的位置, 保证确定的元素左右两边分别>=和<=

int Partition(ElemType list[], int low, int high) {
    ElemType pivot = list[low];
    while (low < high) {
        while (low < high && list[high] >= pivot)
            high--;
        list[low] = list[high];
        while (low < high && list[low] <= pivot)
            low++;
        list[high] = list[low];
    }
    list[low] = pivot;
    return low;
}

void QuickSort(ElemType list[], int low, int high) {
    if (low < high) {
        int pivot_position = Partition(list, low, high);
        QuickSort(list, low, pivot_position - 1);
        QuickSort(list, pivot_position + 1, high);
    }
}

空间复杂度(栈): 最好=平均=log2n, 最坏 = n

时间复杂度: 最坏:每次划分都在端点处 n2, 最好:每次划分都在中点 nlog2n, 平均nlog2n

不稳定

简单选择排序

从未排序序列中找到最小元素, 插入已排序元素之后

void SelectSort(ElemType list[], int length) {
    for (int for_each = 0; for_each < length - 1; for_each++) {
        int min = for_each;
        int unsorted = for_each + 1;
        for (int find_min = unsorted; find_min < length; find_min++)
            if (list[find_min] < list[min])
                min = find_min;
        // get min from unsorted to last
        if (min != for_each)
            swap(list[for_each], list[min]);
    }
}

空间复杂度: 1

时间复杂度: 比较: \(\frac{n(n-1)}2\), 移动最好 0 最坏 3 * (n-1), 总体n2 (移动一次要三次操作)

不稳定

堆排序

大根堆: L(i)>=L(2i) && L(i)>=L(2i+1) 任意节点的值<=父结点的值 i 从 1 开始

小根堆: L(i)<=L(2i) && L(i)<=L(2i+1)

对于最大堆和最小堆，删除操作是针对堆顶元素而言的，即把末尾元素移动到堆顶，再自定向下(重复构建堆的操作)，递归调整。 增加操作是将新元素置于最后

void adjust(ElemType list[], int len, int index) {
    int left = 2 * index;      // index的左子节点
    int right = 2 * index + 1; // index的右子节点

    int max_idx = index;
    if (left < len && list[left] > list[max_idx])
        max_idx = left;
    if (right < len && list[right] > list[max_idx])
        max_idx = right;

    if (max_idx != index) {
        swap(list[max_idx], list[index]);
        adjust(list, len, max_idx);
    }
}

// 堆排序
void heapSort(ElemType list[], int size) {
    // 构建大根堆（从最后一个非叶子节点向上）
    for (int i = size / 2 - 1; i >= 0; i--) {
        adjust(list, size, i);
    }

    // 输出结果
    for (int i = size - 1; i >= 1; i--) {
        swap(list[0], list[i]); // 将当前最大的放置到数组末尾
        adjust(list, i, 0); // 将未完成排序的部分继续进行堆排序
    }
}

空间复杂度: 1

时间复杂度: nlogn

不稳定

归并排序

小组排序, 合并成大组

ElemType assist_array[100]; // length of list
void Merge(ElemType list[], int low, int mid, int high) {
    int low2mid_idx, mid2high_idx, list_idx;
    for (list_idx = low; list_idx <= high; list_idx++)
        assist_array[list_idx] = list[list_idx];
    for (low2mid_idx = low, mid2high_idx = mid + 1, list_idx = low;
         low2mid_idx <= mid && mid2high_idx <= high;
         list_idx++) {
        if (assist_array[low2mid_idx] <= assist_array[mid2high_idx]) //稳定排序
        {
            list[list_idx] = assist_array[low2mid_idx];
            low2mid_idx++;
        } else {
            list[list_idx] = assist_array[mid2high_idx];
            mid2high_idx++;
        }
    }
    while (low2mid_idx <= mid)
        list[list_idx++] = assist_array[low2mid_idx++];
    while (mid2high_idx <= high)
        list[list_idx++] = assist_array[mid2high_idx++];
}

void MergeSort(ElemType list[], int low, int high) {
    if (low < high) {
        int mid = (low + high) / 2;
        MergeSort(list, low, mid);
        MergeSort(list, mid + 1, high);
        Merge(list, low, mid, high);
    }
}

空间复杂度: n

时间复杂度: nlog2n

稳定

基数排序

将关键字拆分为组(如个十百千万) , 每个组排序一次

空间复杂度: r, r 为每个组有多少个可能的值(例如 10)

时间复杂度: d*(n+r), d 是关键字的组数

稳定

image-20231013155743839

排序算法的比较

算法 最好时间 平均时间 最坏时间 空间 稳定
直接插入 n n2/4 n2 1 yes
折半插入 n n2/4
(nlog2n)		 n2 1 yes
希尔 ? n1.3 n2 1 no
冒泡 n-1 n2 n(n-1)/2 1 yes
快速 nlog2n nlog2n n2 log2n
~n		 no
简单选择 n(n-1)/2 n(n-1)/2 n(n-1)/2 1 no
堆 nlog2n nlog2n nlog2n 1 no
归并 nlog2n nlog2n nlog2n n yes
基数 d*(n+r) d*(n+r) d*(n+r) r yes

归并排序:

  1. 将外存文件分成多个文件, 将文件内部依次内部排序, 然后写入外存
  2. 对内部排序后的文件归并, 直到整个文件有序

每一趟归并都需要读一遍所有数据, 写一遍所有数据

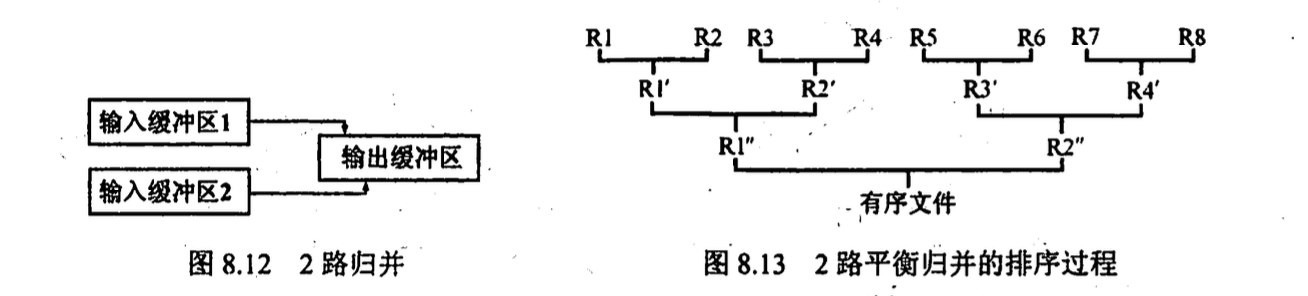
screenshot

如图所示是三次归并

\(外部排序总时间 = 内部排序所需时间+外存信息读写时间+内部归并所需时间\)

多路平衡归并与败者树

路数k增加时, 每趟归并需要进行的比较次数为\((n-1)(k-1)\)

总比较次数就为

\(\lceil log_kr \rceil(n-1)(k-1) = \frac{\lceil log_2r \rceil(n-1)(k-1)}{log_2k}\) n为元素个数, r 为初始分段段数, k 为归并路数, \(\lceil log_kr \rceil\)为归并趟数, 可以得出, 当 k 增加时, 内部排序的时间会增加

败者树: 增加 k 不会增加内部排序比较次数

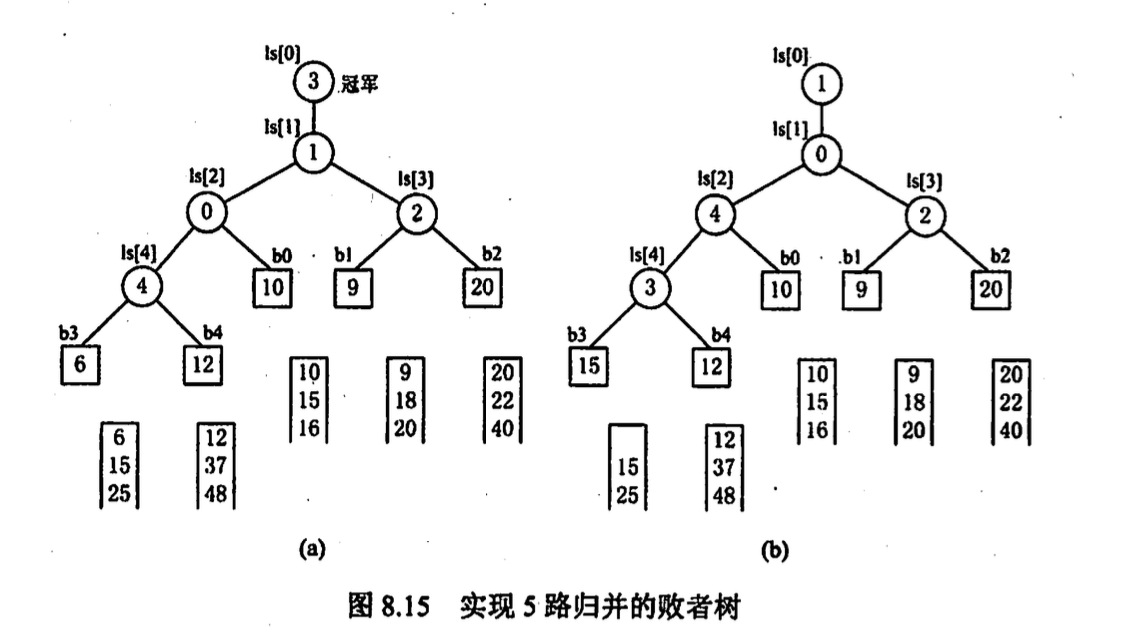
screenshot-5268930

比较次数: \(\lceil log_kr \rceil(n-1) \lceil log_2k \rceil= \lceil log_2r \rceil(n-1)\)

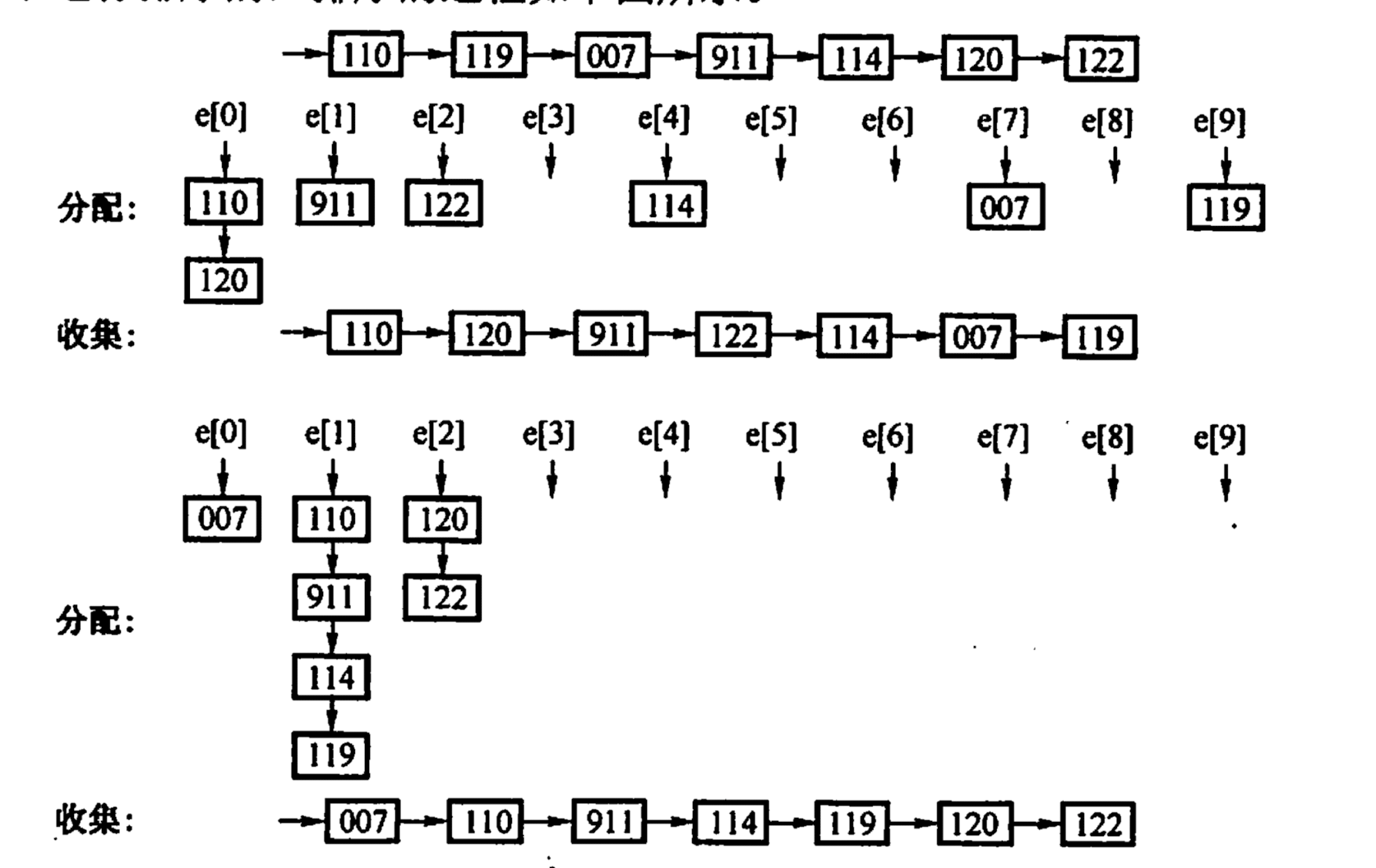
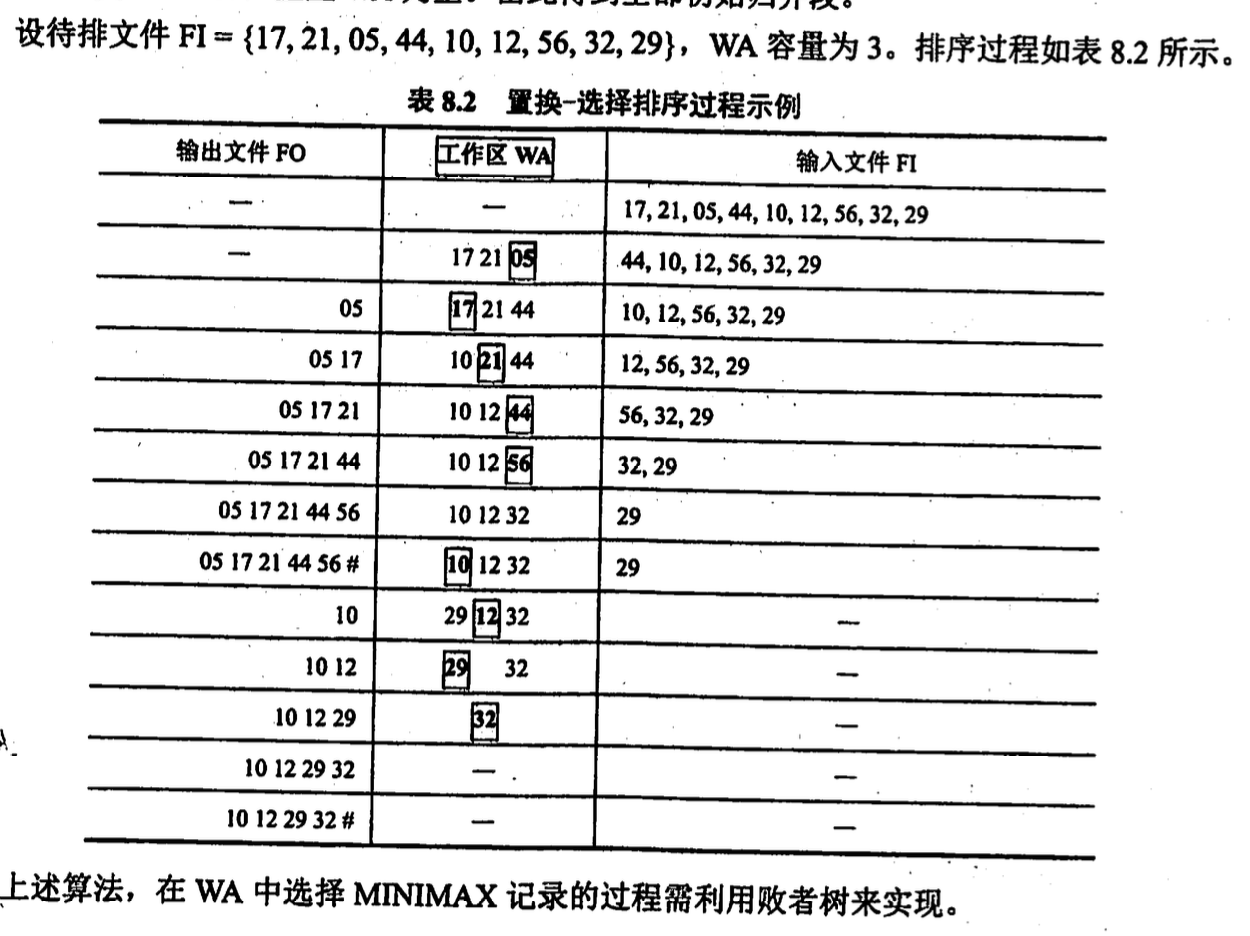
置换-选择排序（生成初始归并段）

考虑到内存大小有限, 为了减少归并段个数 r, 提出本算法

初始待排文件 fi, 初始归并段输出文件 fo, 内存工作区 wa, wa 可以容下 w 个记录, 有以下步骤

  1. 从 fi 输入 w 记录到 wa
  2. 从 wa 中选出关键字最小的记录, 记为 minw (使用败者树)
  3. 将 minw 输出到 fo
  4. 若 fi 不为空, 从 fi输入 1 个记录到 wa
  5. 从 wa 中所有关键字比 minw 大的记录中选择最小的记录, 作为新的 minw
  6. 重复 3~5, 直到 wa 中选不出 minw, 输出一个归并段结束符到 fo
  7. 重复 2~6, 直到 wa 空, 结束
screenshot-5269857

最佳归并树

为了统一置换选择产生的归并段的长度, 做归并平衡, 利用哈夫曼树, 并添加虚段使其是一棵完全树

\(n_0 = (k-1)n_k+1\)

\(n_k = \frac{(n_0-1)}{k-1}\)

其中 k 为叉数

当 \((n_0-1\%{k-1}=u)\) 时, 应该添加\(k-u-1\)个虚段

screenshot-5270469